ИПМ ДВО РАН

Наиболее важные научные результаты ИПМ ДВО РАН

2021г.

1. Для приближенного вычисления кратных интегралов Коробов (1959) и Главка (1962) предложили использовать параллелепипедальные сетки специального вида. Эта идея оказалась плодотворной как с практической, так и с теоретической точек зрения. Она породила целое направление на стыке теории чисел и вычислительной математики. Наибольший интерес представляют сетки с наименьшим отклонением от равномерного распределения. Эти вопросы изучались в работах Коробова, Главки, Зарембы, Нидеррайтера, Кейперса, Ларчера и многих других математиков. Быковский В.А. (2002) получил наилучшую на сегодняшний момент верхнюю оценку для наименьшего отклонения. Из результатов настоящей работы вытекает, что оценка Быковского выполняется для почти всех s-мерных сеток Коробова, состоящих из n узлов, где s>1, а n – простое.

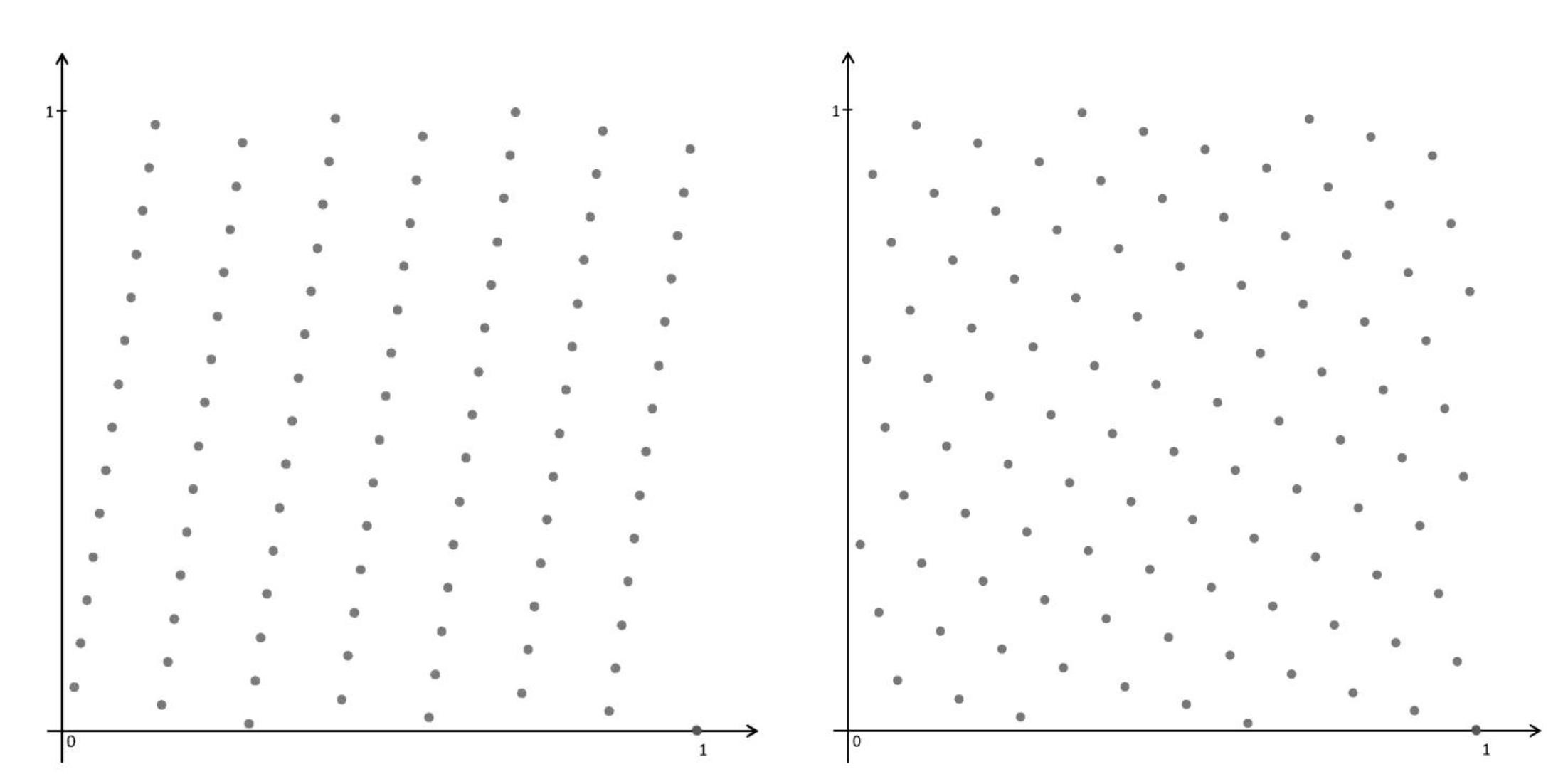
Примеры двумерных сеток Коробова, состоящих из 101 узла

А.А. Илларионов. Вероятностная оценка для отклонений сеток Коробова // Математический сборник. 2021. Т. 212. №11. С. 73–88.

2.Впервые показано, что передний фронт кумулятивной струи, генерируемой при коллапсе парового пузырька в процессе лазероиндуцированного кипения воды с недогревом вновь вторично вскипает. Вторичное вскипание фронта струи создаёт область пониженной плотности, в которой оставшаяся часть струйного потока распространяется без сопротивления, приводя к эффекту суперкавитации. Численно при кипении воды с недогревом в ближайшей окрестности лазерного нагревательного элемента установлен эффект суперкавитации.

Эволюция паровой фазы во времени вблизи торца оптоволокна при нагреве воды лазерным излучением с длиной волны 1.94 мкм и мощностью 10 Вт. Вторичное вскипание струи и последующее схлопывание вторичной паровой фазы показано на кадрах 14 – 26. Время между кадрами 1/50 мс.

Начало процесса вторичного вскипания воды вблизи торца оптоволокна. Время между кадрами (а) и (б) 1.25·10-5. Экспозиция в кадре 2·10-6 с. Скорость съёмки 80000 кадр/с. Диаметр торца кварцевого оптоволокна 400 мкм

V.M. Chudnovskii, M.A. Guzev, V.I. Yusupov, R.V. Fursenko, J. Okajima. Study of methods for controlling direction and velocity of liquid jets formed during subcooled boiling. // International Journal of Heat and Mass Transfer. 2021. V. 173. 121250. https://doi.org/10.1016/j.ijheatmasstransfer.2021.121250 0017-9310
А.А. Чернов, М.А. Гузев, А.А. Пильник, Т.П. Адамова, А.А. Левин, В.М. Чудновский. Влияние вторичного вскипания на динамику струи, формирующейся при коллапсе парового пузырька, индуцированного лазерным нагревом жидкости. // Доклады Российской академии наук. Физика, технические науки. 2021. Т. 501. С. 70-74.

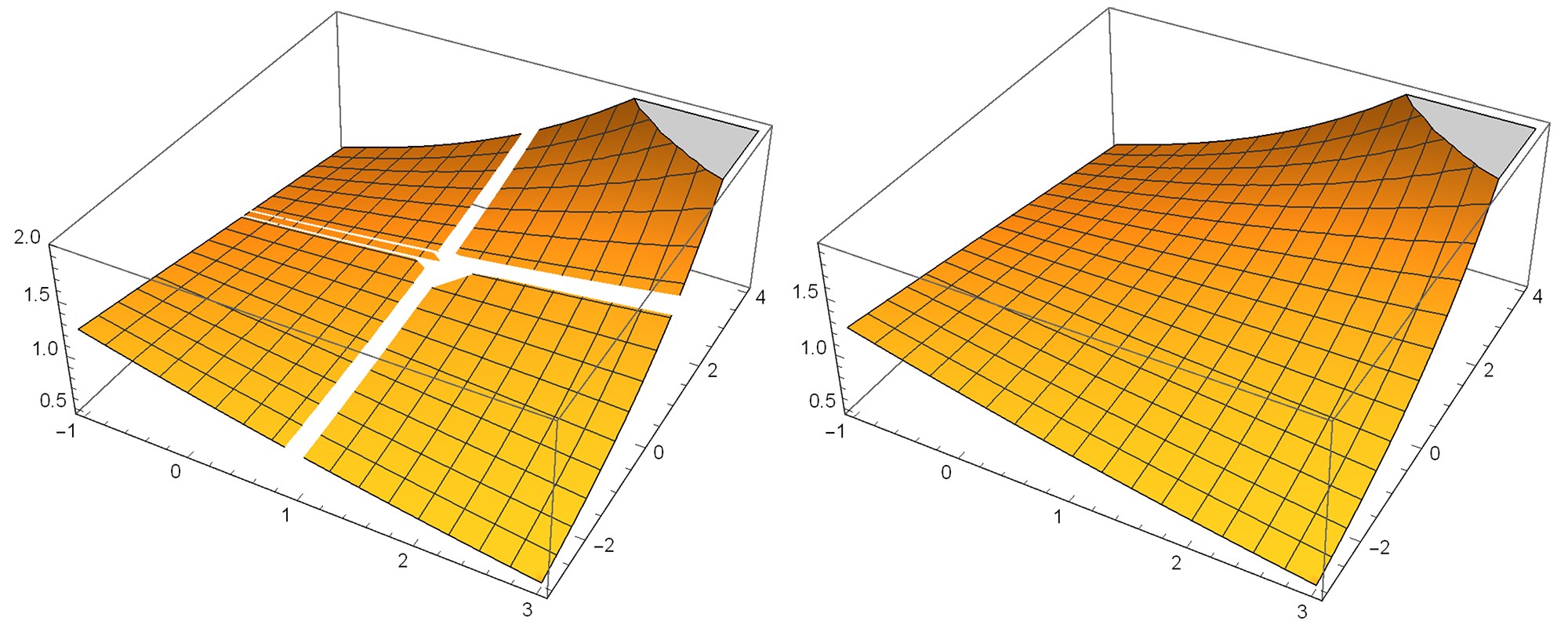
3.Исследованы коэффициентные обратные задачи для моделей распространения акустических, электромагнитных, тепловых и других физических полей в сплошных средах. Указанные задачи возникают при разработке технологий дизайна средств невидимости материальных тел, устройств концентрирования полей и других специальных устройств, служащих для управления физическими полями. Для решения указанных задач предложен эффективный алгоритм, основанный на оптимизационном методе решения обратных задач. Применение разработанного алгоритма позволило спроектировать устройства, обладающие простотой технической реализации и максимальной эффективностью в рассматриваемом классе устройств.

Структура оптимального теплового концентратора (а) и соответствующее поле температуры в его окрестности (б)

Г.В. Алексеев, В.А. Левин, Д.А. Терешко. Анализ и оптимизация в задачах дизайна устройств невидимости материальных тел. М.: ФИЗМАТЛИТ, 2021. 328 с. ISBN 978-5-9221-1919-1
G.V. Alekseev, D.A. Tereshko, Y.V. Shestopalov. Optimization approach for axisymmetric electric field cloaking and shielding // Inverse Problems in Science and Engineering. 2021. V. 29, N1. P. 40-55. (Scopus, WoS) DOI: 10.1080/17415977.2020.1772780

4.По данным ГНСС-измерений исследованы ионосферные возмущения, порожденные сильным эксплозивным извержением вулкана Пик Сарычева, о. Матуа, Курильская островная дуга, произошедшее в период с 11 по 16 июня 2009 года. Получены амплитудно-частотные и скоростные характеристики ковулканических перемещающихся ионосферных возмущений на расстояниях до 1000 км от вулкана. Исследована асимметрия их распространения и зависимость от фонового уровня ионизации ионосферы. Поставлен вопрос о возможностях использования ионосферного ГНСС-зондирования для целей раннего предупреждения о сильных вулканических извержениях.

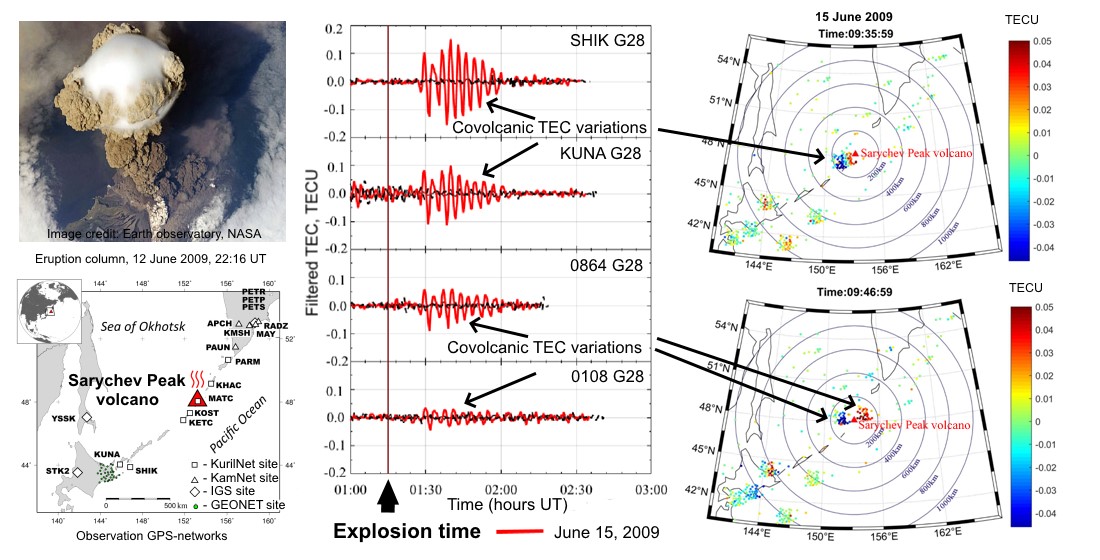
Примеры обнаруженных вариаций полного электронного содержания (ПЭС) и карты распределения вариаций ПЭС вблизи вулкана

Shestakov N., Orlyakovskiy A., Perevalova N., Titkov N.; Chebrov D.; Ohzono M., Takahashi H. Investigation of Ionospheric Response to June 2009 Sarychev Peak Volcano Eruption. // Remote Sensing. 2021. V. 13(4). 638. (WoS, Scopus) https://doi.org/10.3390/rs13040638

2020г.

1. Предложен и обоснован механизм образования микроструи нагретой жидкости на конце оптоволокна, через которое подается лазерное излучение. С помощью численного моделирования были изучены процессы образования и коллапса пузырька испарившейся жидкости и последующее формирование струи нагретой жидкости в зависимости от мощности лазерного излучения и геометрии оптоволокна. Данное исследование, подтвержденное экспериментальными данными, имеет важное значение для развития новых методов лазерной хирургии, позволяющие выполнять хирургические операции практически на любых участках тела, в том числе внутри кровеносных сосудов, без термического повреждения тканей.

Струя нагретой жидкости в эксперименте и схема образования струи.

R.V. Fursenko, V.M. Chudnovskii, S.S. Minaev, J. Okajima. Mechanism of high velocity jet formation after a gas bubble collapse near the micro fi ber immersed in a liquid. // International Journal of Heat and Mass Transfer (2020) 163:120420 (Wos, Scopus) https://doi.org/10.1016/j.ijheatmasstransfer.2020.120420
V.M. Chudnovskii, A.A. Levin, V.I. Yusupov, M.A. Guzev, A.A. Chernov. The formation of a cumulative jet during the collapse of a vapor bubble in a subcooled liquid formed as a result of laser heating //International Journal of Heat and Mass Transfer 150 (2020) 119286 (Wos, Scopus) https://doi.org/10.1016/j.ijheatmasstransfer.2019.119286

2. Изучена группа преобразований гипергеометрических функций 4F3 с единичным сдвигом параметров. Приведен всесторонний анализ структуры подгруппы, порожденной известными преобразованиями. Доказано, что эта подгруппа изоморфна прямому произведению симметрической группы степени 5 и 5-мерной целочисленной решетки, рассматриваемой как группа относительно операции сложения. Установлена связь между двухчленными преобразованиями 4F3 и трехчленными преобразованиями 3F2 и представлен метод вычисления коэффициентов отношений смежности для функций 3F2, вычисленных в единице. Получен класс формул суммирования, связанных с элементами рассматриваемой группы. Данное исследование имеет важное значение при описании симметрий теории Клебша-Гордана.

Пример аналитического продолжения гипергеометрической функции как функции от параметров

D.B. Karp, E.G. Prilepkina, Transformations of the hypergeometric 4F3 with one unit shift: a group theoretic study, Mathematics, 2020, 8(11), 1966. DOI:10.3390/math8111966

3. Решена задача удаления из орграфа минимального числа ребер, изолирующих некоторое подмножество вершин. Эта задача вызвана широко распространенными сейчас мерами изоляции в транспортных, экономических, медицинских, образовательных и др. сетях. Первоначально она ставилась с целью локализации в белковой сети пораженных белков, перекрывая пути прохождения сигналов через них, и выглядела как NP-полная. Требование минимальности числа удаляемых ребер связано с необходимостью наименьшим образом деформировать исходную сеть. Последовательными преобразованиями орграфа в двухполюсники эта задача сведена к задаче о минимальном разрезе и максимальном потоке. Была проведена апробация построенного алгоритма на белковой сети Арабидопсис с 190 вершинами и 619 ребрами.

На рисунках иллюстрируются начальный (слева) и конечный (справа) шаги преобразования орграфа в двухполюсники. На рисунке слева в исходном орграфе черным цветом выделены помеченные вершины. На рисунке справа показаны два двухполюсника с источниками и стоками в виде квадратов, в которых ищутся максимальные потоки и минимальные разрезы

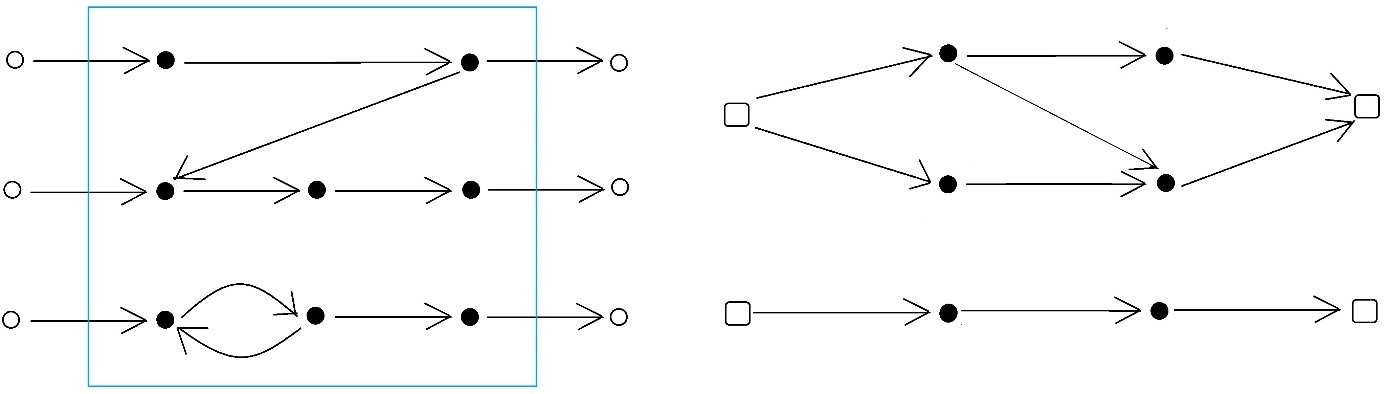
Г.Ш. Цициашвили. Вычислительная сложность оптимального блокирования заданных вершин в орграфе// Дальневосточный математический журнал. 2020. Т. 20. №2.
G.Sh. Tsitsiashvili, M.A. Osipova, A.S. Losev, Yu.N. Kharchenko. Computational complexity of optimal blocking of a subset of vertices in a directed graph. CoMeSySo, 2020. AISC 1295.

2019г.

Теоретическая математика..

Доказана явная формула для третьего момента центральных значений автоморфных L-функций ассоциированных с примитивными параболическими формами уровня один и большого веса. Полученная в результате явная формула содержит главный член, предсказанный гипотезой из теории случайных матриц, и остаточный член, выраженный через интеграл от произведения четвертой степени модуля дзета-функции Римана и гипергеометрической функции 3F2. Как следствие получена новая верхняя оценка на рассматриваемый третий момента, улучшающая предыдущий результат Пенга. Кроме того, мы получаем новую оценку сверху на рост центральных значений рассматриваемых L-функций при весе, стремящемся к бесконечности.

(Фроленков Д.А. The cubic moment of automorphic L-functions in the weight aspect. // J. Number Theory. 2020. 207:2. С. 247–281, DOI: https://doi.org/10.1016/j.jnt.2019.07.009)

Математическое моделирование.

>Выполнен теоретический и численный анализ непрерывной стационарной модели переноса кислорода в тканях мозга человека. Рассматриваемая модель представляет собой краевую задачу для системы нелинейных эллиптических уравнений для концентраций кислорода в крови и в ткани. Доказана однозначная разрешимость краевой задачи и сходимость итерационной процедуры нахождения решения. Численные эксперименты продемонстрировали согласованность модели.

(Kovtanyuk, A.E., Chebotarev, A.Y., Botkin, N.D., Turova, V.L., Sidorenko, I.N., Lampe, R. Continuum model of oxygen transport in brain // Journal of Mathematical Analysis and Applications. 2019. 474, pp. 1352–1363. https://doi.org/10.1016/j.jmaa.2019.02.020)