ИПМ ДВО РАН

Наиболее важные научные результаты ИПМ ДВО РАН

2022г.

Теоретическая математика

1.Получены новые верхние оценки наименьшего отклонения для приближенного вычисления кратных интегралов при помощи параллелепипедальных сеток специального вида. Доказано, что оценка Быковского выполняется для почти всех s-мерных сеток Коробова, состоящих из n узлов, где s>2, при произвольном натуральном n. Ранее такой результат был получен автором для простого n. Также были получены новые результаты, связанные с распределением сеток Коробова. Из них вытекает, что для почти всех сеток Коробова оценка Быковского является неулучшаемой. Полученный результат имеет фундаментальное значение для развития решетчатого метода Больцмана в задачах гидродинамики многофазных течений, задачах смачивания и растекания, а также при описании оптимальных микроструктурных свойств композиционных и функционально-градиентных материалов.

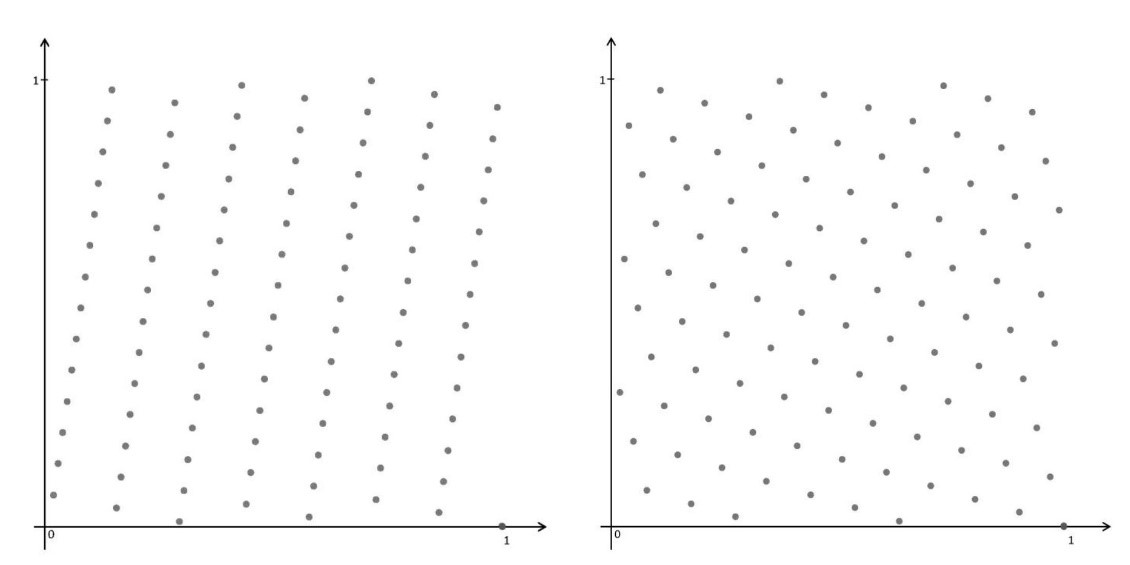
Примеры двумерных сеток Коробова, состоящих из 101 узла

А.А. Илларионов. Распределение последовательностей Коробова–Главки // Математический сборник. 2022. Т. 213, № 9. С. 70–96.

2.Работа посвящена шашкам Фейнмана – элементарной модели движения электрона, предложенной Р. Фейнманом. В этой игре шашка движется согласно простым правилам по клетчатой доске, а мы следим за ее поворотами.

Пример движения шашки Фейнмана

Шашки Фейнмана также известны как одномерное квантовое блуждание или модель Изинга при мнимой температуре. В статье приведено математическое доказательство гипотезы Фейнмана 1965 г. о том, что эта дискретная модель (при больших временах, малой средней скорости и малом размере клетки) согласована с непрерывной. Исследованы асимптотические свойства модели (при малом размере клетки и больших временах), усилены результаты Дж. Нарликара 1972 г. и Т. Сунады и Т. Татэ 2012 г. Впервые отмечена и доказана концентрация меры в пределе при уменьшении размера клетки. Производено вторичное квантование модели. Приведён обзор известных результатов о шашках Фейнмана.
М. Б. Скопенков, А. В. Устинов. Шашки Фейнмана: к алгоритмической квантовой теории. // Успехи математических наук. 2022. 77:3(465). С. 73–160.

Прикладная математика

1.Выполнено математическое моделирование процесса распространения затопленной нагретой струи внутри замкнутой полости, заполненной холодной жидкостью. Показано, что время переноса тепла к границе существенно меньше времени нагрева жидкости в объеме. Феноменологические параметры модели были определены на основе сопоставления с данными экспериментального исследования. Полученные результаты были использованы для обоснования хирургического лечения сосудистых аномалий.

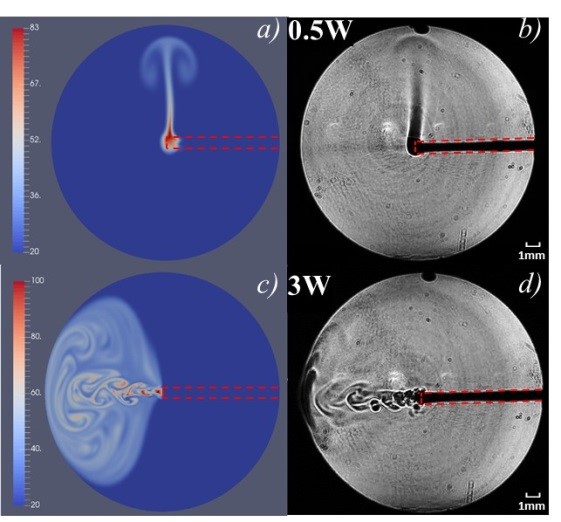
Распределение температуры полученное численным моделированием (слева) и соответствующие экспериментальные теневые изображения (справа). a) Рассчитанное поле температур в случае свободной конвекции, b) теневое изображение, полученное из эксперимента при мощности лазерного излучения 0.5W, c) поле температур, рассчитанное в случае генерации микроструй в режиме пузырькового кипения, d) теневое изображение полученное из эксперимента при мощности лазерного излучения 3W. Контур оптоволокна выделен красной прерывистой линией

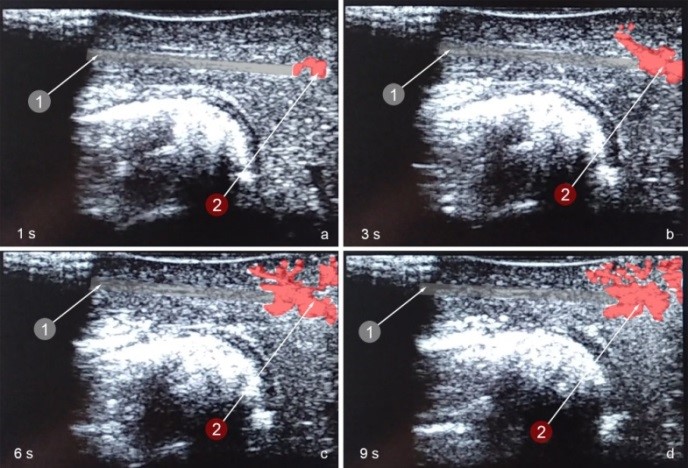
Эхограмма кипения крови в окрестности торца оптоволокна в сосудах печени кролика в различные моменты времени на 1, 3, 6 и 9 секунде от начала действия лазерного излучения с длиной волны 1.9 мкм. Цифрой (1) показано оптоволокно диаметром 400 мкм, а цифрой (2) область кипения, заполненная парогазовыми пузырьками (выделено красным цветом). Веерное распространение пузырьков газа по сосудам в сторону от очага прогрева указывает на движение потоков разогретой крови, в которых движутся пузырьки.

С.Н. Мокрин, академик РАН М.А. Гузев, Д.А. Терешко, А.В. Кулик, С.С. Минаев, И.А. Абушкин, В.М. Чудновский. Селективный лазерный нагрев оболочек замкнутых полостей, заполненных жидкостью. // Доклады Российской академии наук. Физика, технические науки. 2022. Т. 507. С. 68-72.
И.А. Абушкин, В.М. Чудновский, М.А. Гузев, Ю.А. Поляев, Р.В. Гарбузов. Лазерная внутритканевая термотерапия в хирургическом лечении сосудистых аномалий. // Бюллетень экспериментальной биологии и медицины. 2022. Том 174, № 9. С. 396-400.
А.В. Кулик, С.Н. Мокрин, А.М. Краевский, С.С. Минаев, М.А. Гузев, В.М. Чудновский. Особенности динамики струйного потока, генерируемого при поверхностном кипении жидкости на лазерном нагревателе. // Письма в журнал технической физики. 2022. Т. 48, вып. 2. С. 20-23.

2.Предложен новый подход к изучению моделей статистической физики, на примере частного случая спинового стекла Эдвардса-Андерсона на квадратной двумерной решетке спинов Изинга. Показано, что конфигурации и энергию основных состояний систем спинового стекла можно предсказать с помощью нейронной сети. Проведено сравнение полученных результатов нейросети ограниченной машины Больцмана с точными и приближенными вычислительными методами. Предлагаемый метод вычисления основного состояния показал более высокую точность по сравнению с гибридным методом Монте-Карло, методами полного перебора и трансфер-матриц. Применение нейронных сетей выглядит многообещающим для изучения сложных спиновых систем больших размерностей и позволяют значительно улучшить результаты теоретических исследований, проводимых классическими вычислительными методами.

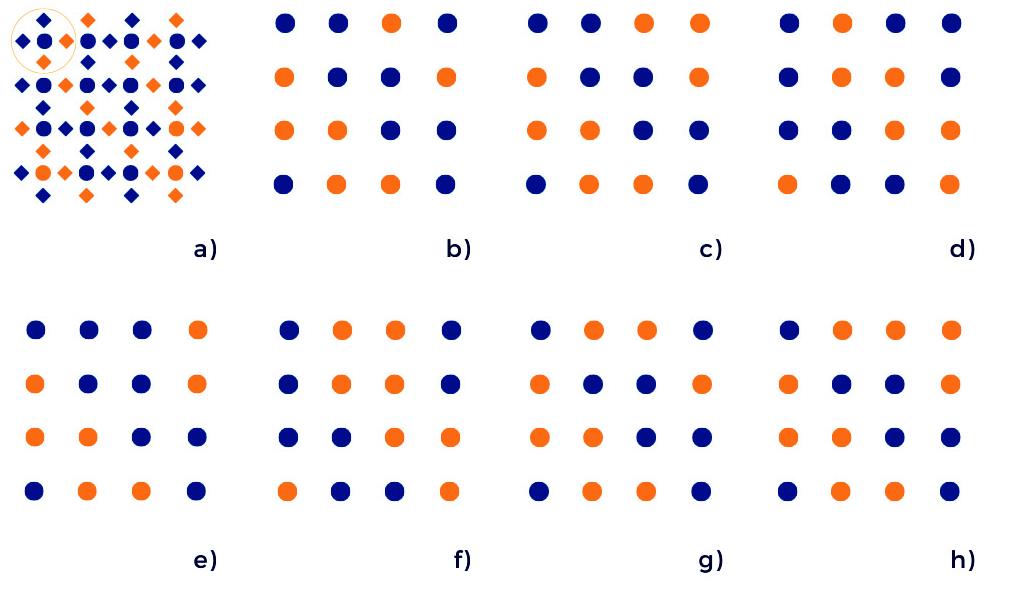
Пример системы для обучения (a) и основные состояния (b-h) системы 4x4 при заданном распределении связей.

А.О. Король, В.Ю. Капитан, А.В. Пержу, М.А. Падалко, Д.Ю. Капитан, Р.А. Волотовский, Е.В. Васильев, А.Е. Рыбин, П.А. Овчинников, П.Д. Андрющенко, А.Г. Макаров, Ю.А. Шевченко, И.Г. Ильюшин, К.С. Солдатов. Вычисление основных состояний спиновых стекол с использованием ограниченной машины Больцмана. // Письма в Журнал экспериментальной и теоретической физики. 2022. Том 115, № 8. С. 500–504.

3.В рамках математической модели, базирующейся на нестационарном уравнении переноса излучения, предложен новый экстраполяционный алгоритм улучшения качества томографических изображений коэффициента ослабления излучения, основанный на облучении исследуемой среды серией импульсов различной длительности. Проведенный на известном тест-фантоме численный анализ предложенного алгоритма подтвердил его эффективность для фильтрации паразитного влияния рассеяния при рентгеновской томографии неоднородных сред.

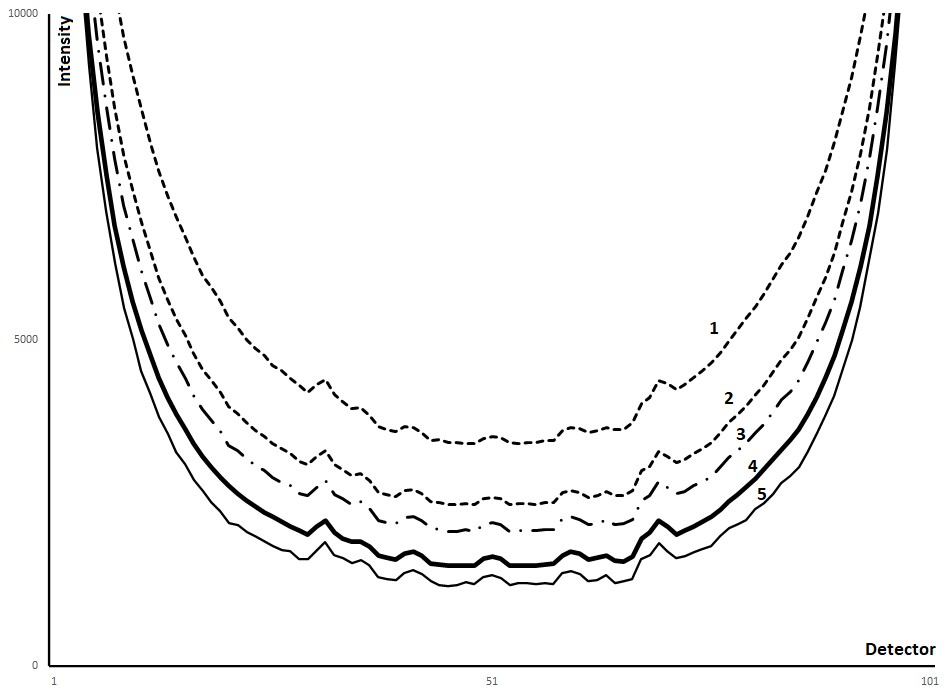
Пунктирными линиями 1, 2 изображены проекции, соответствующие выходящему излучению для источников излучения с длительностью импульсов 300 пс и 100 пс, соответственно. Жирная непрерывная линия 4 соответствует «идеальной» проекции без рассеяния. Штрихпунктирная линия 3 получена в результате линейной экстраполяции проекций. Тонкая непрерывная линия 5 соответствуют проекции, полученной путем экстраполяции с помощью асимптотической по длительности импульса формуле.

Рисунок 7 - На рисунке (а) изображено внутреннее строение структуры фантома в заданной плоскости. На рисунках (b), (c) приведены результаты реконструкции коэффициента ослабления μ при облучении импульсами длительности 1=300 и 2=100 пикосекунд, соответственно. На рисунке (d) приведены результаты восстановления функции μ с использованием процедуры экстраполяции выходящего сигнала.

Прохоров И.В., Яровенко И.П., Повышение качества томографических изображений при облучении среды импульсами различной длительности // Доклады Российской академии наук. Математика, информатика, процессы управления. 2022. Т. 505. С. 71-78.