ИПМ ДВО РАН

Наиболее важные научные результаты ИПМ ДВО РАН

2023г.

Теоретическая математика

1.Рассмотрены последовательности элементов произвольного (в том числе и конечного) поля, удовлетворяющие нелинейным разложениям билинейного типа. В случае поля комплексных чисел такого вида последовательности возникают при изучении последовательностей Сомоса и решении функциональных уравнений, связанных с многомерными (векторными) теоремами сложения. Доказаны теоремы о существовании и единственности последовательностей в случае задания начальных данных, не содержащих "много" нулей. Полученные результаты использованы для построения аналогов криптографических алгоритмов Диффи-Хеллмана и Эль-Гамаля. Задача дискретного логарифмирования ставится в группе, состоящей из последовательных четверок элементов, указанных выше последовательностей, групповая операция определяется как S(n+m) = S(n)+S(m), где S(n) - четверка с номером n.

Алгоритм Диффи-Хелмна без формул

2.Разработан математический аппарат решения задач дизайна устройств маскировки и экранирования материальных тел относительно магнитных и электрических полей, основанный на оптимизационном методе. На его основе предложена математическая технология решения указанных задач дизайна в случае, когда искомое проектируемое устройство состоит из конечного числа кольцевых или сферических слоев, заполненных искомыми материалами. Уникальность данной технологии состоит в том, что лежащий в ее основе численный алгоритм использует предварительно установленные важные свойства оптимальных решений и, в частности, свойство релейности, продемонстрированное на рис. 1. Кроме того, указанная технология применима при использовании для маскировки как изотропных, так и анизотропных сред. Основной результат, отличающий разработанную технологию от других методов дизайна, состоит в том, что она позволяет проектировать маскировочные устройства, обладающие, с одной стороны, простотой технической реализации, а, с другой стороны, наивысшей эффективностью в рассматриваемом классе устройств.

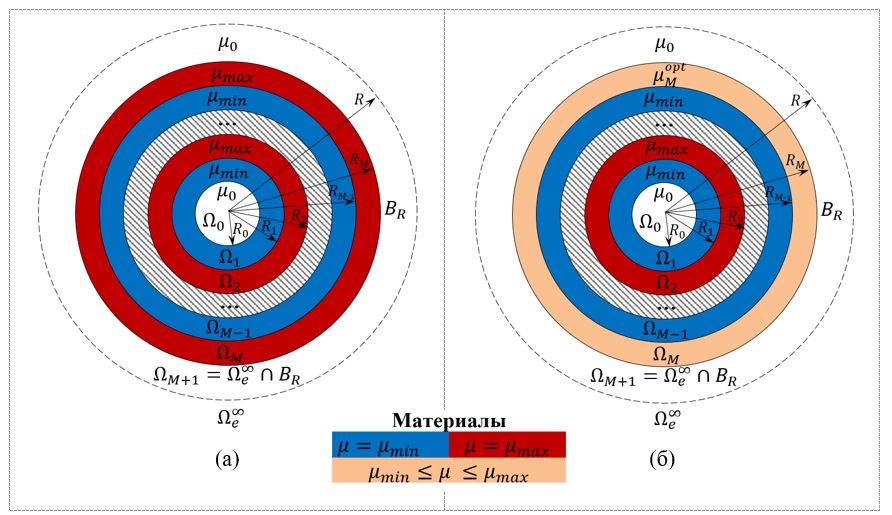
Схематическое изображение оптимальных многослойных изотропных оболочек, полученных с помощью решения задач экранирования (а) либо маскировки (б) для пары значений μ_min=0.0045 и μ_max=70, отвечающих магнитным проницаемостям инженерного сверхпроводника и кобальта, соответственно.

Alekseev G.V., Lobanov A.V. Optimization Method for Solving Cloaking and Shielding Problems for a 3D Model of Electrostatics // Mathematics. 2023. 11(6). P. 1395:1-17. (Q1, WoS, Scopus, RSCI)
Спивак Ю.Э. Численная оптимизация в задачах проектирования многослойных магнитных маскировочных оболочек // Дальневосточный математический журнал. 2023. Т. 23, N 2. (RSCI, РИНЦ)

Прикладная математика

1.Экспериментально и численно исследован рост и схлопывание кавитационного пузырька при лазерном нагреве и вскипании с недогревом воды в окрестности кончика оптоволокна (лазерном нагревательном элементе), установленного в заполненной водой стеклянной трубке с двумя открытыми концами. Кавитация, инициированная непрерывным лазерным излучением, сопровождается выталкивающим и втягивающим движением разогретой жидкости в трубке и за ее пределами. Впервые показано, что в трубке с установленным лазерным нагревательным элементом в потоке жидкости, движущейся за стенками пузырька, при его схлопывании на удаленном от торца полюсе поверхности пузырька возникает струя, направленная через пузырек к торцу оптоволокна. Струя ускоряет процесс всасывания жидкости в трубку. Эффект выталкивания и последующего всасывания разогретой жидкости в трубку может иметь большое практическое значение в технических и медицинских приложениях, в частности, для санации поверхности и при лечении ран.

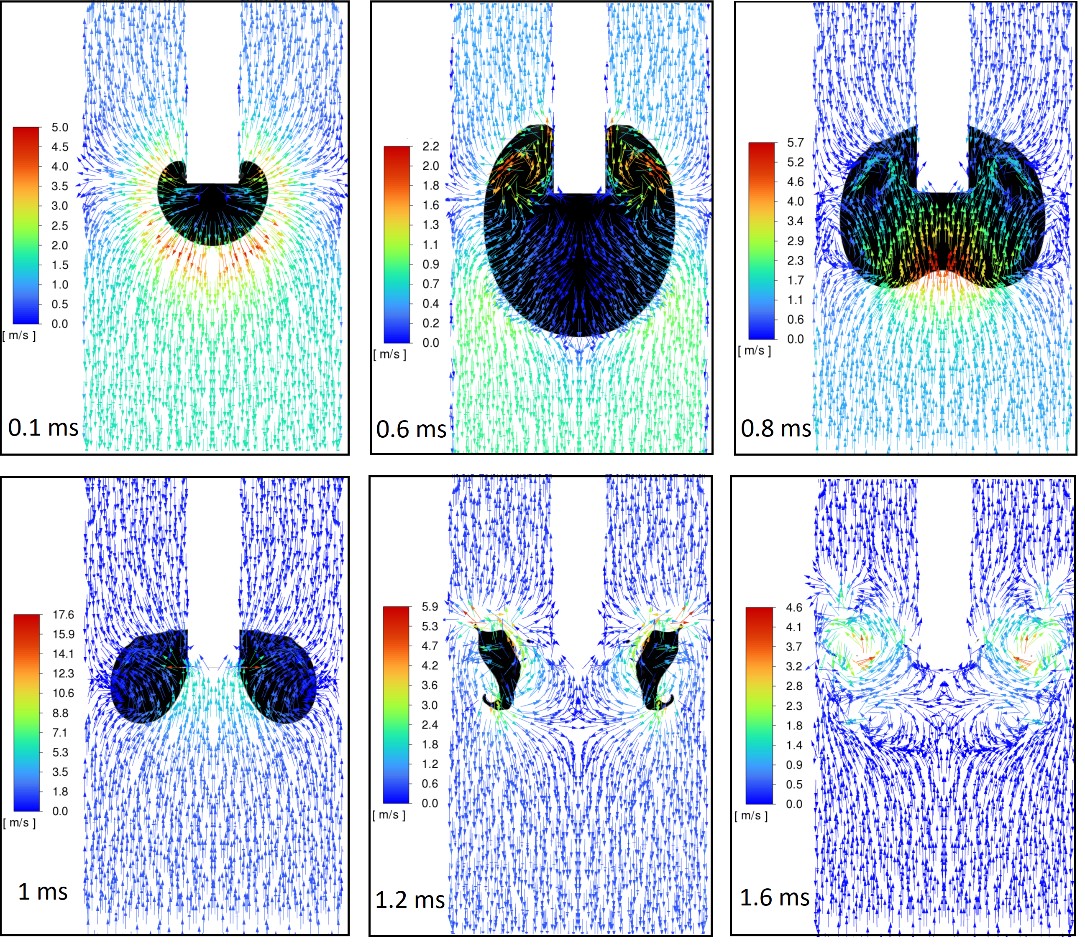
Поле скоростей в процессе моделирования роста схлопывания пузырька в трубке. Черным цветом отмечена газовая фаза.

В.М. Чудновский, академик РАН М.А. Гузев, Е.П. Дац, А.В. Кулик. Эффект ускоренного всасывания жидкости в трубке при лазерной кавитации в лазерном нагревательном элементе. // Доклады Российской академии наук. Физика, технические науки. 2023. Т. 513.
Е.П. Дац, А.В. Кулик, М.А. Гузев, В.М. Чудновский. Особенности динамики струйного потока, генерируемого при поверхностном кипении жидкости на лазерном нагревателе. // Письма в журнал технической физики. 2023. Т. 49, вып. 16. С. 38-41.

2.В работе представлен новый кластерный алгоритм Монте-Карло для проведения суперкомпьютерных расчетов численного моделирования в магнитных системах. В силу особенностей реализации, метод наиболее эффективен для моделей с ограниченным радиусом взаимодействия. Алгоритм основан на сочетании случайного выбора спинового кластера методом Монте-Карло и полного перебора всех состояний выбранного кластера. Работоспособность метода протестирована в следующих моделях: ферромагнитной модели Изинга, модели спинового стекла Эдвардса-Андерсона, дипольного спинового льда на гексагональной и пентагональной каирских решетках.

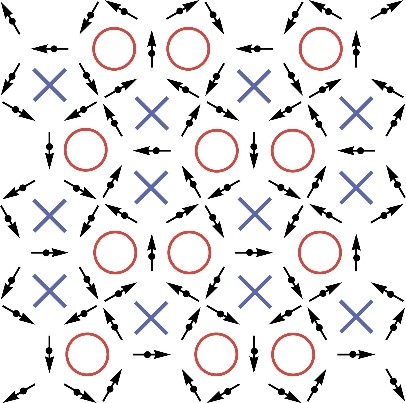
Каирская решетка с Изинг-подобными точечными диполями.

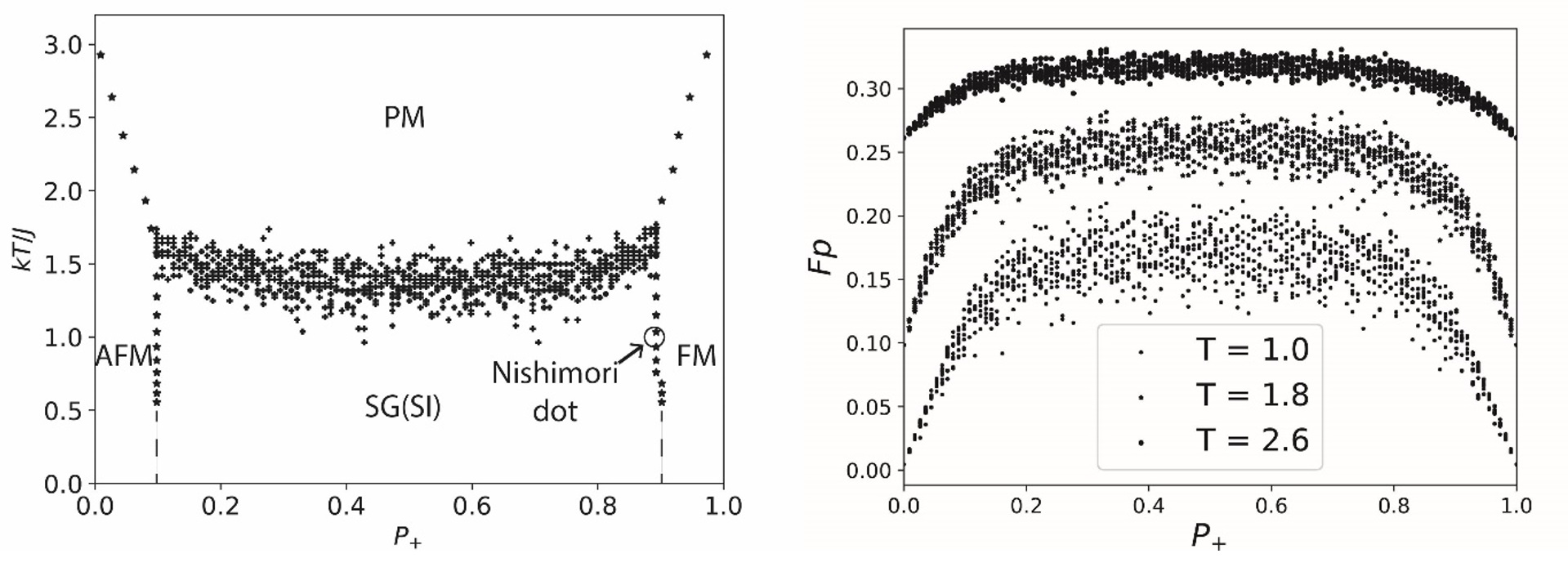
Фазовая диаграмма и параметр фрустрации образцов без внешнего поля

Были получены фазовые диаграммы для парамагнетика (область PM), спинового стекла (область SG(SI)), ферромагнетика (область FM), антиферромагнетика (область AFM) (рис. 2 слева). Представлены значения критических температур решеток в зависимости от геометрической конфигурации и степени разбавления системы ферромагнитными связями. Также представлены зависимости поведения параметра фрустрации решетки при разных температурах (правая часть рис. 2). Разработанный метод имеет перспективу дальнейшего его применения в вычислительной математике для проверки сходимости других методов, основанных на марковских цепях.

Makarova K. et al. Canonical Monte Carlo multispin cluster method //Journal of Computational and Applied Mathematics. – 2023. – V. 427. – P. 115153.

3.В медицине актуальной задачей является распознавание фатального исхода при лечении пациентов от COVID-19. Для обработки информации, состоящей из 24 признаков, для пациентов, входящих в группу повышенного риска (с опухолевыми заболеваниями крови), авторами был применен оригинальный метод интервального распознавания образов. Пациентов разбили на группы и у пациентов с фатальным исходом выделили по каждому признаку интервал его изменения. Такие пациенты распознавались, если значения 24 признаков попадали в эти интервалы. Наихудшее качество распознавания K (частота правильного распознавания) в 3-ей группе (см. табл. 1) удалось улучшить с 0,77 до 0,98 при ее разбиении на подгруппы (до 69 лет и старше 69). Для оценки влияния отдельного признака на качество распознавания введена (см. табл. 2) информативность признака (частота правильного распознавания исхода этим признаком). Метод интервального распознавания образов, вследствие своего быстродействия, оказался эффективным при обработке больших данных, а в совокупности с оценкой информативности признаков дает возможность медикам получить общую картину прогнозных выводов.

Качество распознавания фатального исхода в выделенных группах.

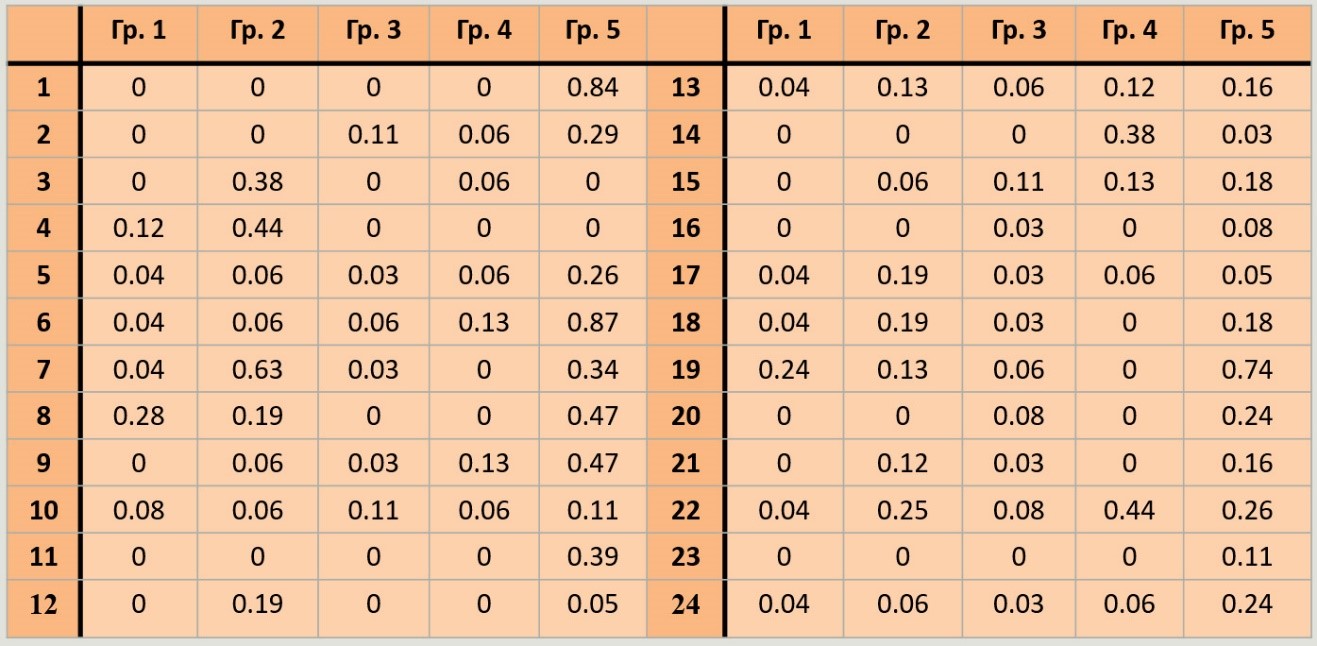
Информативность 24 признаков в выделенных группах.

Tsitsiashvili G.Sh., Nevzorova V.A., Talko A.V., Osipova M.A. Interval Pattern Recognition to COVID 19 Patients // Reliability: Theory and Applications, 2023, v 2 (73), pp. 73-78.